Multiplikacja (efekt działania procentu składanego)

         Efekt multiplikacji to inaczej efekt działania procentu składanego. Polega na tym, że odsetki naliczone w danym okresie odsetkowym (zazwyczaj rocznym) są kapitalizowane, czyli dodawane do kapitału. W następnym okresie odsetkowym, odsetki naliczane są od tego powiększonego kapitału (pierwotny kapitał plus wypracowane odsetki) - są więc wyższe. Powtarzany mechanizm powoduje zwiększanie się kapitału oraz odsetek. Teoretycznie, może być dowolna ilość okresów odsetkowych. Może być jeden okres - wtedy odsetki naliczane są na koniec okresu, mogą być dwa - wtedy odsetki są naliczane i kapitalizowane po upływie połowy roku, a później drugi raz po upływie roku. Może też być ich nieskończenie wiele - wtedy mamy do czynienia z kapitalizacją ciągłą. Należy jednak mieć świadomość, że dzielenie roku na okresy kapitalizacji to również podział stopy procentowej, ale o tym szczegółowo później. Efekt działania procentu składanego jest często wykorzystywany w reklamie, np. slogan pt. „u nas kapitalizacja minutowa”. Trudno oprzeć się podejrzeniu, że służy jedynie zwabieniu mniej świadomych amatorów szybkiego zysku. Bo czy kapitalizacja minutowa rzeczywiście przynosi nadzwyczajny efekt finansowy? Zobaczmy.

Jeśli wpłacimy 1.000 PLN na roczną lokatę, oprocentowaną R = 8% z kapitalizacja roczną, po roku otrzymamy odsetki:

1.000 PLN × 0,08 = 80 PLN

Jeśli będziemy podwajać ilości kapitalizacji (n) w roku (okresy odsetkowe), otrzymamy następująca tabelę oraz wykres:

  

Widać wyraźnie z tabeli oraz wykresu przyrostu odsetek, że zwiększanie ilości kapitalizacji zwiększa efekt finansowy, ale praktycznie przy 128 kapitalizacjach dalsze zwiększanie ilości nie ma już znaczenia. Podwojenie ilości odsetek podwyższa efekt finansowy jedynie o 0,01 PLN. Podobnie jest z dalszym zwiększaniem ilości kapitalizacji.

         Zobaczmy, jak zmieni się sytuacja, jeżeli dwukrotnie zwiększymy stopę procentową (R).

         Wynik zmienił się, ale przyrosty odsetek, związane z ilością kapitalizacji pozostały bez zmian. Zmiana ilości kapitalizacji ze 128 na 4.096, a więc 32 krotna daje jedynie przyrost o 0,12 PLN.

         Byłem kiedyś świadkiem jak w banku starszy pan awanturował się, bo zwabiony reklamą i obietnicą odsetek 10% zdeponował na 2 miesiące 10.000 PLN. Spodziewał się odsetek 1.000 PLN, a bank naliczył mu jedynie 166,67 PLN. Wynika to oczywiście z faktu, że 10% to nominalna stopa procentowa R, która zawsze dotyczy roku. Jeśli mamy do czynienia z okresami krótszymi niż rok (n > 1) stopa „R” ulega podziałowi na odpowiednią stopę "r" podokresu „n”.

W tym wypadku (starszego pana), na horyzoncie 2 m-cy oprocentowanie wynosiło  r% = R% × 2/12, czyli 10% × 1/6 = 1.67%, a wiec 10.000 PLN × 0,0167 = 166,67 PLN

 

Powyższa tabela zawiera standardowe ilości kapitalizacji (od rocznej = 1, do ciągłej). Oprocentowanie zwiększyłem do 100% dla lepszej czytelności wykresu. Widać wyraźnie, że w naszym przykładzie zwiększanie ilości kapitalizacji do dobowej (czyli codziennej) włącznie przynosi istotny przyrost odsetek. Dalsze zwiększanie ilości kapitalizacji nie powoduje już znaczącego przyrostu  efektu finansowego. Powodem jest wspomniany podział nominalnej stopy procentowej na okresy kapitalizacji. Dla przykładu nominalna stopa R = 10% dla dnia wynosi w przybliżeniu 0,03%, a dla godziny 0,001%. Kapitał 10.000 PLN w ciągu dnia wypracuje 2,78 PLN, a w ciągu godziny 0,11 PLN odsetek. 

         A jak wygląda związek efektu multiplikacji z czasem?

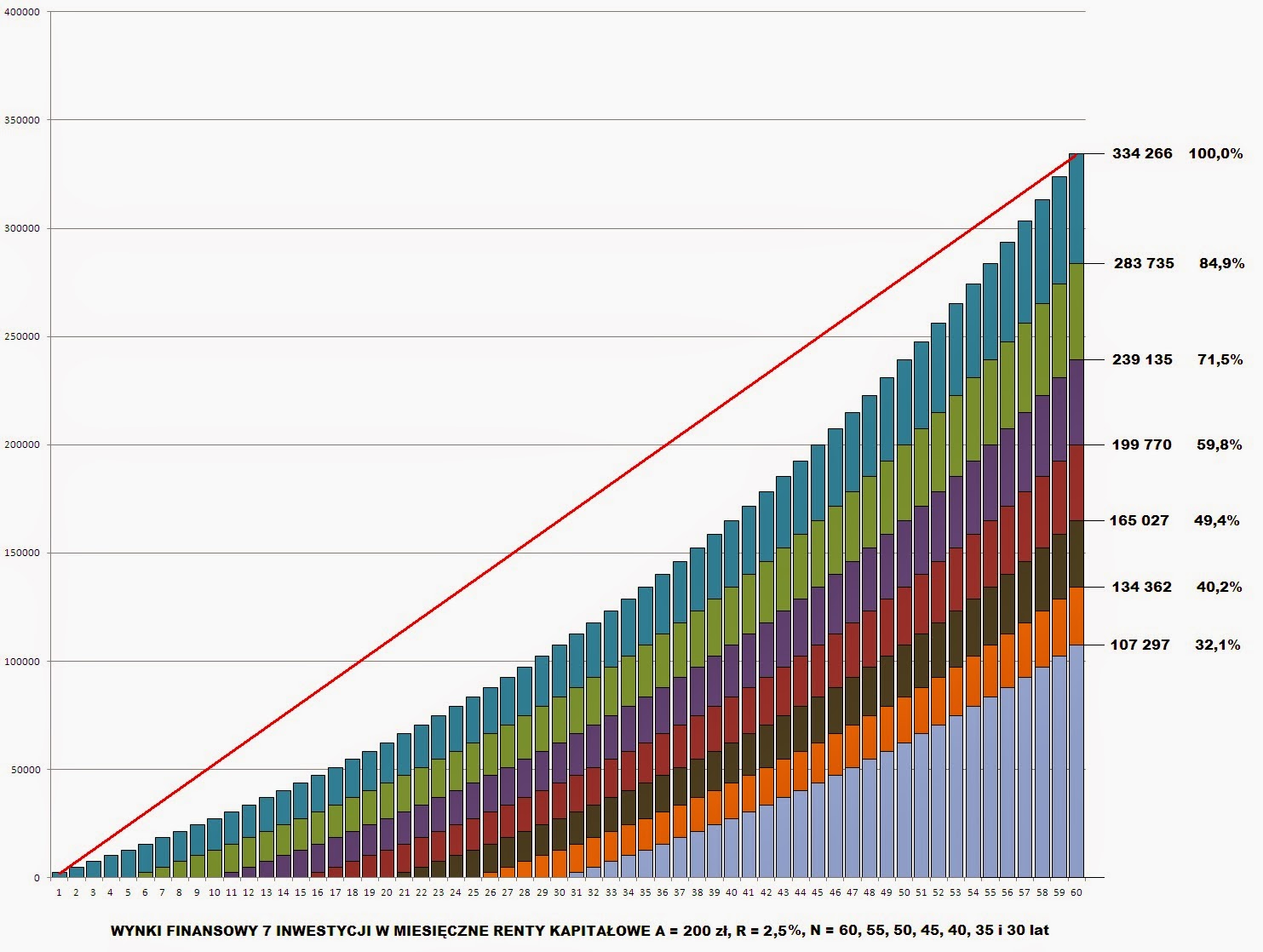
Powyższy wykres przedstawia efekty finansowe prostego odkładania (nie ma odsetek i nie uwzględniamy inflacji) miesięcznych rent kapitałowych A = 200 PLN przez 60, 55, 50, 45, 40, 35 i 30 lat. Wyniki to odpowiednio od 144.000 PLN, do 72.000 PLN. Wynik jest efektem prostego iloczynu ilości miesięcy i rent A = 200 PLN.

Włączmy teraz do tego schematu oprocentowanie R = 2,5% w stosunku rocznym.

        

         Wynik wyraźnie ukazuje efekt działania procentu. Zauważmy też, że pomimo złudzenia optycznego, poszczególne wykresy maja dokładnie taki sam kształt - są jedynie przesunięte względem siebie na poziomej osi czasu. Inwestowanie przez 30 lat to 50% czasu inwestowania przez 60 lat, ale wynik 107.297 PLN to tylko 32,1% wyniku inwestowania przez 60 lat. Opóźnienie rozpoczęcia inwestowania o 10 lat (nieco ponad 8% czasu) powoduje to, że wynik jest o 15% niższy.

         Zastosujmy teraz oprocentowanie 10%.

Tu widać już większy efekt finansowy, ale i znacznie większe różnice spowodowane czasem inwestowania. Przy tym oprocentowaniu powstrzymanie się od inwestowania o 10 lat daje już stratę 40% względnej wartości.

         Warto też wskazać pewną właściwość efektu działania procentu składanego. Jeśli ustalimy moment w przyszłości kiedy wartość inwestycji stanowi podwojenia kapitału IC i obliczymy czas do tego momentu, to okazuje się, że po upływie następnego takiego odcinka czasu kapitał znów się podwoi. Czyli podwojenie kapitału następuje w równych odstępach czasowych, których długość jest oczywiście uzależniona do stopy procentowej i ilości kapitalizacji. Im większa efektywna stopa procentowa EAR, tym krótsze odcinki czasowe, po upływie których następować będzie podwojenie kapitału. Ale nie musi to być podwojenie. W przypadku podwojenia mnożną jest kapitał IC, a mnożnikiem liczba 2, ale może być inna odpowiednia liczba - większa od jedności.

Opisaną prawidłowość ilustruje poniższy wykres:

         Można obliczyć termin, po którym wartość inwestycji będzie stanowiła odpowiednią krotność kapitału IC, np. 2-krotną.

Wzór wykorzystuje niejednokrotnie już wcześniej używany współczynnik przyszłej wartości FVF:

Ilość dni, po upływie których kapitał osiągnie wartość FV = 365  × (ln(FV / PV)) / ln(FVF)

Przykład:

Kapitał IC = 1.000 PLN zainwestowano w instrument, przy R = 8% i n = 12. Po ilu dniach wartość kapitału FV będzie równa 2.000 PLN, czyli w tym przypadku podwoi się?

Najpierw obliczamy FVF = (8% / 1200 +1)¹² = 1,0829981  (EAR = 8,23%)

FV / PV = 2.000 PLN / 1.000 PLN = 2

ln(2) / ln (1,0829981) = 0,693147 / 0,0797332 = 8,6933297

365 × 8,6933297 = 3.173 dni

Po upływie 3.173 dni wartość instrumentu osiągnie 2.000 PLN. Po 6.346 dniach osiągnie wartość 4.000 PLN, po 9.519 dniach wartość 8.000 PLN, itd.


A teraz porównajmy dwóch inwestorów inwestujących w renty kapitałowe A = 100 PLN.

          Inwestor pierwszy inwestuje przez 60 lat miesięczne kwoty A = 100 PLN przy oprocentowaniu 6%. W ciągu 60 lat (720 miesięcy) inwestuje w sumie kapitał 72.000 PLN. Wartość inwestycji po 60 latach wynosi 708.955,30 PLN. Zauważmy, że stopa APR = 885%!

         Drugi inwestor B inwestuje tak samo, ale rozpoczyna inwestowanie po 10 latach. Inwestuje w sumie 60.000 PLN, a wartość inwestycji wynosi 380.612,70. Stanowi to 55% wartości inwestycji pierwszego inwestora. Stopa APR = 534%. Zauważmy, że czas utrzymywana inwestycji B jest tylko o 1/6 (ok. 16.6%) krótszy od A, zainwestowany kapitał mniejszy o 17% od A, ale wynik finansowy różni się aż o 45%. To właśnie niewykorzystany efekt multiplikacji.

         Gdyby drugi inwestor chciał przez 50 lat inwestowania osiągnąć taki sam wynik finansowy musiałby inwestować renty A = 186,27 i w sumie zainwestować kapitał 111.762 PLN. Opisane zależności ilustruje poniższy wykres.

Gdyby natomiast chciał zainwestować w ciągu tych 50 lat taki sam kapitał, musiałby inwestować renty kapitałowe w wysokości A = 120 PLN. Wynik byłby na poziomie 456.735,24 PLN, a stopa APR = 644%.

         I na koniec jeszcze jedno zestawienie.

         I tym razem mamy do czynienia z inwestycją na horyzoncie 30 lat. Miesięczne renty kapitałowe A = 100 PLN a oprocentowanie R = 12%. Porównanych jest 6 inwestycji od A do F. Pierwszy (A) inwestuje przez 30 lat, wartość jego inwestycji po 30 latach wynosi 352.991 PLN. Drugi (B) rozpoczyna inwestycje z 5-letnim opóźnieniem i każdy następny rozpoczyna inwestycje 5 lat później. Inwestor B traci na 5-letnim opóźnieniu w stosunku do inwestora A 157.228 PLN. Inwestor C traci na 10-letnim opóźnieniu w stosunku do inwestora A 284.534 PLN, itd. Stopa zwrotu z inwestycji A wynosi 881%, a inwestycji B rozpoczętej 5 lat później tylko 533%. Zwróćmy też uwagę na straty miesięczne, dzienne i godzinowe (ostatnie 3 wiersze tabeli). Np. inwestor B w czasie 5 lat (60 miesięcy), w których nie inwestował tracił 2.620 PLN na miesiąc, 86 PLN na dobę i 3,59 na godzinę.

         Podsumowując należy stwierdzić, że efekt procentu składanego zwiększa się w czasie w związku z tym korzystne jest jak najwcześniejsze rozpoczęcie inwestycji. Podkreślić trzeba, że efekt multiplikacji dotyczy jedynie instrumentów finansowych opartych na stopie procentowej. Zwracam na to uwagę, ponieważ bardzo często przebiegli "doradcy finansowi" nakłaniając klienta do inwestowania posługują się "magią procentu składanego". Opisują jego działanie, zbawienne dla pieniędzy klienta efekty i potrzebę długoterminowego utrzymywania inwestycji dla uruchomienia multiplikacji. Problem jedynie w tym, że omawiane inwestycje nie mają nic wspólnego ze stopą procentową i efektem multiplikacji.