Portfel akcji i ryzyko

         Na początek kilka słów na temat ryzyka. Warto o nim wspomnieć, ponieważ powszechne rozumienie ryzyka może być dla inwestora mylące. Mówimy często, że ktoś ryzykuje, a ryzyko jest tym większe, im większa możliwość, że wydarzy się coś złego. Ryzykowne jest kupowanie produktu nieznanej firmy, bo może się popsuć. Ryzykowne jest uprawianie spadochroniarstwa albo wspinaczki, bo można się zabić.
         Nieco inaczej rozumiemy ryzyko inwestycyjne w finansach. Jeśli ktoś oszacował stopę zwrotu na poziomie 25, a zrealizował 40, to oczywiście odnotuje to z radością i satysfakcją - uzyskał więcej niż na to liczył. W takim wyniku kryje się jednak inna cenna informacja, której nie wolno przeoczyć, a mianowicie informacja o istniejącym ryzyku. Ryzyko inwestycyjne rozumiemy jako prawdopodobieństwo uzyskania wyniku innego niż przewidywany. To ryzyko może być negatywne, ale może też być pozytywne - jak w tym przypadku. Prawdopodobieństwo uzyskania wyniku 40 (25 + 15) było takie samo jak uzyskanie wyniku 10 (25 - 15).

         Aby przybliżyć nieco problematykę związaną z oceną rentowności, szacowaniem ryzyka oraz analizą i metodami wyboru instrumentów finansowych posłużymy się przykładem najbardziej typowych i najbardziej ryzykownych instrumentów rynku kapitałowego, jakimi są akcje spółek.

         Dodam jeszcze, że całkowite ryzyko, z jakim mamy do czynienia przy inwestowaniu nie jest pojęciem jednolitym i składa się z dwóch różnych rodzajów ryzyka. Pierwsze z nich związane jest z funkcjonowaniem całego rynku i nazywa się ryzykiem systematycznym. Drugie ryzyko specyficzne związane jest wyłącznie z działalnością danej spółki akcyjnej, której walory analizujemy. Wzajemny udział obu składników decyduje o tym, czy akcje danej spółki zaliczymy do defensywnych (przewaga ryzyka rynkowego systematycznego) czy ofensywnych (przewaga ryzyka rynkowego specyficznego). Jak się dalej przekonamy, ryzyko inwestycyjne można obniżyć – teoretycznie nawet do zera, ale dotyczy to tylko ryzyka specyficznego. Nie jesteśmy natomiast w stanie obniżyć ryzyka systematycznego, na które nie mamy wpływu, a na które niestety inwestor zawsze jest narażony.

         Każdego inwestora interesuje możliwie największa stopa zwrotu z inwestycji oraz najmniejsze ryzyko. Jak wspomniałem, regułą jest wzrost ryzyka przy zwiększaniu stopy zwrotu i odwrotnie. My jednak, wbrew tej regule spróbujemy obniżyć ryzyko inwestycyjne bez obniżania stopy zwrotu. W tym celu stworzymy tzw. portfel akcji. Będzie prosty, bo dwuskładnikowy, ale wystarczy do zilustrowania strategii.

         Przy wyborze akcji danej spółki stoimy przed problemem oceny stopy zwrotu jakiej możemy oczekiwać z inwestycji. Nazywamy ją oczekiwana stopą zwrotu ER (Estimated Rate). Najprostszym metodą obliczenia ER jest założenie, że wysokość stopy zwrotu w przyszłości będzie się kształtowała podobnie jak w przeszłości. Przy takim założeniu można posłużyć się wspomnianą już średnią arytmetyczną, którą oznaczamy symbolem x. Obliczamy ją z historycznych (zrealizowanych) stóp zwrotu . Trzeba zaznaczyć, że ta metoda sprawdza się przy względnej stabilności rynku, ale może okazać się zawodna przy jej braku. Przyjmując średnią x jako oczekiwaną stopę zwrotu musimy mieć świadomość, że zawsze istnieje prawdopodobieństwo uzyskania innego wyniku niż oczekujemy. Jak oszacować tę ewentualną rozbieżność.

         Już wiemy, że ocena wielkości tej rozbieżności to właśnie ocena ryzyka inwestycyjnego - jednego z najważniejszych parametrów inwestycji. Jedną z metod oceny ryzyka jest zastosowanie odchylenia standardowego historycznych stóp zwrotu.

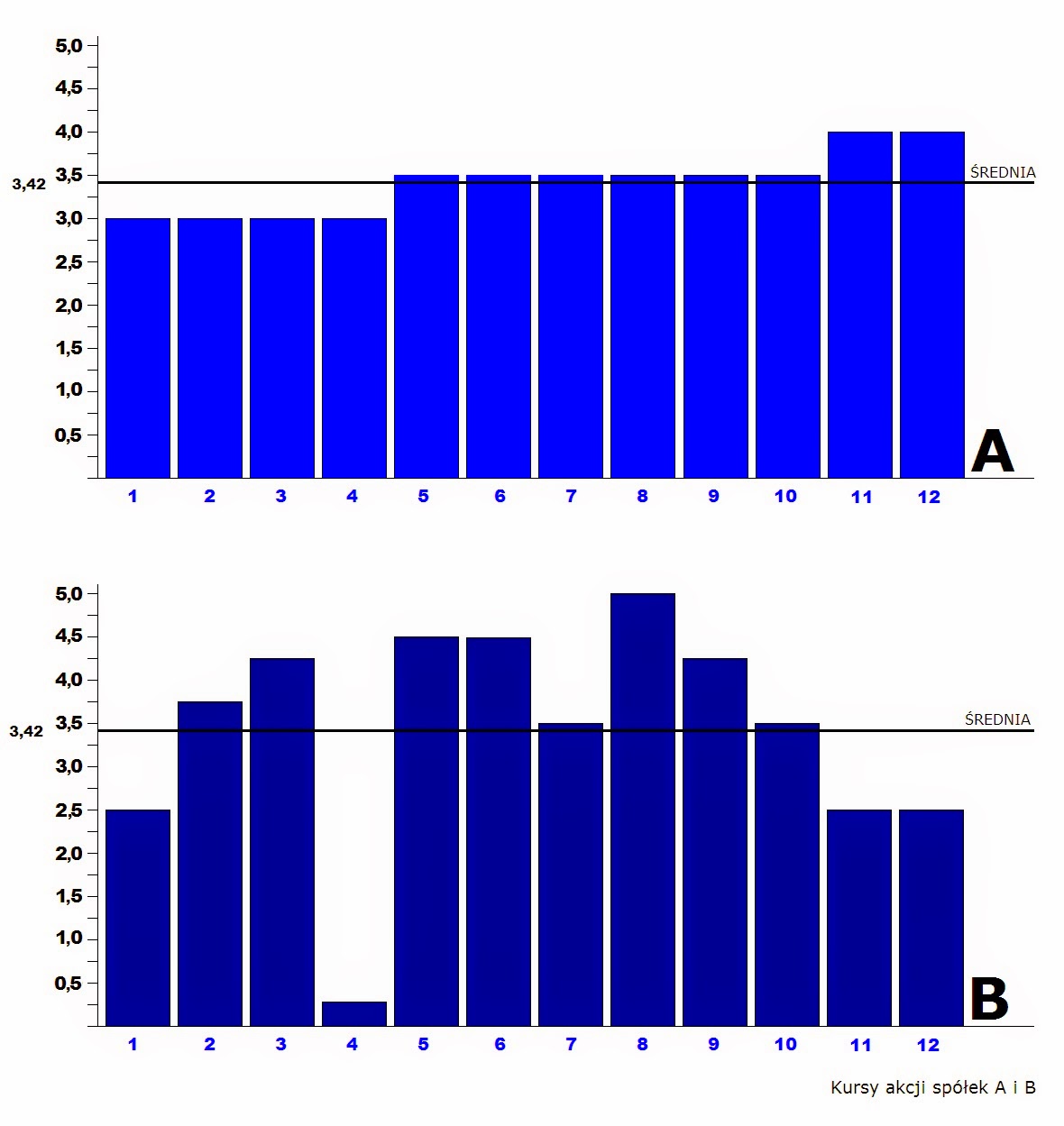
         Powyższy wykres przedstawia historyczne (zrealizowane) miesięczne stopy zwrotu spółek A i B z okresu 12 miesięcy.

Jeśli obliczmy średnie arytmetyczne x  stóp zwrotu obu spółek i wykreślimy j na wykresie, otrzymamy dwie poziome linie:

         Okazuje się, że średnie w obu przypadkach są takie same i wynoszą x  = 3,42. Kierując się średnią, można by stwierdzić, że w obu przypadkach najbardziej prawdopodobnym przyszłym wynikiem jest 3,42. Czy tak jest w istocie. Wystarczy przyjrzeć się wykresowi żeby zauważyć, że nie. Wyniki spółki B są bardziej zróżnicowane, niestabilne, a więc mniej przewidywalne niż spółki A.

         Obliczmy odchylenia poszczególnych wyników od średniej, czyli odchylenie standardowe dla obu spółek.

         Odchylenie standardowe σ to miara średniego odchylenia wyników od obliczonej średniej arytmetycznej x  = 3,42.

Oblicza się je w następujący sposób:

Najpierw należy podnieść do 2. potęgi różnice poszczególnych wyników i średniej.

Np. dla spółki B

1. miesiąc: (3,42 - 2,5)² = 0,8464 lub (2,5 - 3,42)² = 0,8464 - wynik jest taki sam

2. miesiąc: (3,75 - 3,42)² = 0,1089

…

12. miesiąc: (2,5 - 3,42)² = 0,8464

Następnie otrzymane wyniki należy zsumować:

0,8464 + 0,1089 + … + 0,8464 = 185,9

Wynik 185,9 należy podzielić przez (n-1), gdzie n jest ilością miesięcy:

185,9/11 = 16,9

Następnie z 16,9 należy wyciągnąć pierwiastek kwadratowy:

√16,9 = 1,30

Wynikiem jest σ = 1,30, czyli odchylenie standardowe dla spółki B.

Otrzymany w taki sam sposób wynik dla spółki A wynosi σ = 0,36

Jeśli teraz na wykresie zaznaczymy średnie powiększone i obniżone o 1 σ, otrzymamy:

         Interpretacja wyników obliczeń jest następująca. Obliczona średnia to oczekiwana stopa zwrotu ER. Uznajemy, że taki wynik jest najbardziej prawdopodobny. Statystycznie rzecz ujmując można oczekiwać, że prawdopodobieństwo otrzymania wyniku od x -1σ do x -1σ (czyli 3,08 - 3,79 dla A i 2,12 - 4,72 dla B) i wynosi ok. 68%.  Istnieje również prawdopodobieństwo, że wynik będzie jeszcze bardziej odchylony od średniej, a więc od x -2σ do x -1σ  lub x +1σ do x +2σ, ale jest mniejsze i wynosi ok. 27%. Jeszcze większe odchylenia o następną wartość σ  też są możliwe, ale jeszcze mniej prawdopodobne, bo wynoszą ok. 4,4%, ... itd.

         Ogólne ryzyko można obniżyć, ale tylko obniżając ryzyko specyficzne - to już wiemy, ale jak to zrobić. Okazuje się, że można tego dokonać inwestując w akcje więcej niż jednej spółki. Nazywamy to inwestycją portfelową. Czym należy kierować się przy ich wyborze? Otóż na rynku mamy do czynienia z akcjami spółek należących do różnych sektorów gospodarki i w związku z tym występują pewne prawidłowości. Okazuje się bowiem, że np. wzrost cen paliw powoduje wzrost stóp zwrotu akcji spółek należących do sektora paliwowego, ale jednocześnie powoduje spadek stóp zwrotu akcji spółek należących do sektora transportowego i odwrotnie. Mamy więc do czynienia z taką zależnością, że gdy ceny jednych akcji rosną, drugich spadają i odwrotnie. Siłę tego związku można obliczyć i w tym celu stosuje się tzw. współczynnik korelacji. Obliczając korelację stóp zwrotu akcji dwóch spółek możemy otrzymać wynik w zakresie od -1 do 1. Im wynik jest bliższy -1, tym silniejsza jest korelacja ujemna (czyli zależność odwrotna) i tym samym mniejsze jest ryzyko portfela. Wynik 0 oznacza brak korelacji, czyli zależności liniowej charakterystycznej, np. dla akcji spółek sektora odzieżowego i spożywczego. Rezultatem doboru akcji spółek jest otrzymanie portfela o obniżonym ryzyku określanego skrótem MVP (Minimum Variance Portfolio).

         Większość stóp zwrotu z akcji spółek jest niezbyt mocno i raczej dodatnio skorelowanych ze sobą. Wynik dodatni oznacza taką zależność liniową, że gdy rosną ceny jednej akcji, rosną również drugiej, a moc tej zależności jest tym większa, nim współczynnik korelacji jest bliższy jedności (1). Podkreślam jednak wyraźnie, że mówimy o zależności liniowej, a to oznacza, że zerowy wynik korelacji wskazuje jedynie na brak zależności liniowej i nie wyklucza istnienia powiązań o charakterze nieliniowym. Obliczeń korelacji nie będę opisywał ponieważ są skomplikowane. Można je wykonać, np. wykorzystując kalkulator finansowy, albo funkcję MS Excel.

Wklejam natomiast dla ilustracji zrzut ekranowy kalkulatora MVP-2.

Mamy na wejściu dane w postaci zrealizowanych stóp zwrotu 3 spółek A, B i C z 12 miesięcy. Na ich podstawie kalkulator oblicza dla każdej spółki oczekiwaną stopę zwrotu ER, odchylenie standardowe σ  oraz dolne i górne odchylenie od stopy oczekiwanej ER - σ i ER ₊ σ. Następnie oblicza korelację 3 portfeli utworzonych na zasadzie „każdy z każdym”. Widać, że najbliższy -1 jest współczynnik korelacji obliczony dla pary B i C - wynosi -0,56. Z akcji spółek B i C kalkulator tworzy 2-elementowy portfel akcji oraz oblicza optymalny skład procentowy portfela w stosunku 56,1% akcji spółki B i 43,9% akcji spółki C.

Zwróćmy uwagę na to, że σ tak utworzonego portfela wynosi 1,37. Porównując ten wynik  z σ(B) = 2,66 oraz z σ(C) = 3,22 widać wyraźnie, że utworzenie portfela spowodowało znaczące obniżenie ryzyka.

         W praktyce tworzy się portfele wieloskładnikowe. Przykład fragmentu kalkulatora MVP wyświetlającego graficzny wynik takich obliczeń zamieszczam poniżej.

Na wykresie widać wynik utworzenia portfela z akcji 6 wybranych spółek A, E, F, G, H i I. Kalkulator wyświetla wynik dla średniego portfela (jednakowy udział wszystkich spółek - pierwszy słupek od lewej - przezroczysty wykres), wyniki dla poszczególnych akcji oraz dla 6-elementowego portfela utworzonego na zasadzie analizy korelacji oraz doboru % składu poszczególnych spółek do portfela. Obliczenia wymagają rachunku macierzowego, więc nie będę ich tu omawiał. Zwróćmy uwagę na to, że dla średniego portfela ER = 10,868, a σ = 22,012. Gdyby utworzyć portfel o równym składzie akcji spółek ER = 10,868 i z prawdopodobieństwem 68% wynik będzie mieścił się w przedziale -11,144 do 32,880. Jak widać jest możliwość zrealizowania ujemnej ER, czyli straty. Utworzenie portfela znacząco zmniejszyło ryzyko. Spodziewany wynik mieści się w przedziale 4,284 do 18,258. Prawdopodobieństwo zrealizowania ujemnej ER znacząco spadło.   

         Podsumowując należy podkreślić, że racjonalnie działający inwestor powinien wybierać z rynku akcje spółek o najniższym ryzyku (najmniejszym σ), najwyższej oczekiwanej stopie zwrotu ER i jednocześnie takie, które są najmniej ze sobą skorelowane, tzn. mające współczynnik korelacji możliwie bliski -1, albo przynajmniej bliskie 0.

         I jeszcze jedna ważna uwaga na koniec. Prawdą jest fakt, że w miarę wydłużania czasu utrzymywania inwestycji (horyzontu inwestycyjnego) rośnie ryzyko. Ale stosunek wartości oczekiwanej (wyniku finansowego z inwestycji) do ryzyka inwestycji rośnie w czasie. Jeśli wiec inwestujemy w ryzykowne instrumenty (akcje) powinniśmy zastosować dłuższy horyzont czasowy - długoterminowe inwestycje znacznie ograniczają ryzyko. Obserwacja rynku kapitałowego wskazuje na to, że przy wydłużaniu horyzontu inwestycyjnego obniża się prawdopodobieństwo, że stopy zwrotu z akcji w tym okresie będą ujemne. Istnieje też statystyczna prawidłowość, że przy rocznej inwestycji prawdopodobieństwo osiągnięcia premii niższej od zera wynosi ok. 36%. To oznacza, że tylko raz na trzy lata można się spodziewać ujemnej lub zerowej premii. Z tego wniosku powstała najprostsza strategia inwestowania w rynek akcji, która brzmi BUY AND HOLD (kup i trzymaj)